티스토리 뷰
3차원 컴퓨터 그래픽에서 행렬(matrix)은 비례나 회전, 이동같은 기하학적 변환을 간결하게 서술하는 데 쓰이며, 점이나 벡터의 좌표를 한 기준계에서 다른 기준계로 변환 하는 데에도 쓰입니다. 위키피디아에서는 다음과 같은 글로 행렬의 정의를 시작합니다 :
수학에서, 행렬(行列, 영어: matrix) 은 수 또는 문자를 괄호 안에 직사각형 형태로 배열한 것이다.
정의
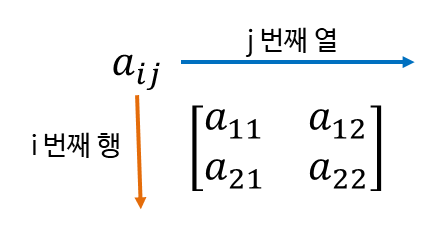
행렬 : m x n 행렬 M 은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열입니다.
차원 : 행(row)들의 개수와 열(column)들의 개수의 곱을 행렬의 차원이라고 부릅니다(행이 4개, 열이 4개일 때 차원은 4 x 4입니다).
원소(element) : 행렬을 구성하는 수들을 원소(element), 또는 성분(entry)라고 합니다. 행렬의 한 성분을 나타내기 위해서 는 행과 열 번호를 아래 첨자로 지정한 Mij 형태로 표기합니다(i : 행, j : 열).
행벡터(row vector)와 열벡터(column vector) : 행렬 중에서 행이 하나인 행렬을 행벡터, 열이 하나인 행렬을 열벡터 라고 합니다. 이러한 벡터는 특별한 행렬로 취급하는데, 이들이 벡터를 행렬 형태로 표기할 때 쓰이기 때문입니다.
행렬의 연산
행렬의 연산 중에서 상등, 덧셈, 스칼라 곱셈, 뺄셈 연산이 있으며 이들의 연산에 대한 정의는 다음과 같습니다 :
- 상등(equal) : 두 행렬은 오직 대응되는 성분들이 상등일 때에만 상등입니다. 두 행렬의 상등을 비교하려면 두 행렬의 행 개수들과 열 개수들이 같아야 합니다(즉, 두 행렬의 차원이 같아야 합니다).
- 덧셈 : 두 행렬을 더할 때는 대응되는 성분들을 더합니다. 덧셈을 수행하기 위해서 두 행렬의 차원은 같아야 합니다.
- 스칼라 곱셈 : 행렬에 하나의 스칼라를 곱할 때는 행렬의 모든 성분에 스칼라를 곱합니다.
- 뺄셈 : 행렬의 뺄셈은 스칼라 곱셈과 행렬 덧셈으로 정의할 수 있습니다. 즉, A - B = A + (-1 * B) = A + (-B) 입니다.
행렬의 덧셈과 곱셈의 성질
행렬 덧셈과 스칼라 곱셈은 성분별로 이루어지므로, 행렬 덧셈과 스칼라 곱셈은 실수의 덧셈 및 곱셈의 성질들을 만족합니다.
- 덧셈의 교환법칙 : A + B = B + A
- 덧셈의 결합법칙 : (A + B) + C = A + (B + C)
- 행렬들에 대한 스칼라의 분배법칙 : r(A + B) = rA + rB
- 스칼라들에 대한 행렬의 분배법칙 : (r + s)A = rA + sA
행렬 곱셈
행렬 A 가 m x n 행렬이고 B가 n x p 행렬이면 둘의 곱 AB 를 정의할 수 있습니다. 이 때 곱 AB 는 한 개의 m x p 행렬이 됩니다. 이 결과를 C라고 할 때, C의 ij 번째 성분은 A의 i번째 행벡터와 B의 j번째 열벡터의 내적입니다.
Cij = Ai,* · B*,j (여기서 *는 와일드카드입니다)
즉, 행렬 A, B 의 곱 AB가 정의되려면 A의 열 수와 B의 행 수가 같아야 합니다. 즉, A의 행벡터들의 차원과 B의 열벡터들의 차원이 같아야 합니다.
또한, 위의 정의로 인해서 곱 AB가 가능하다고, 곱 BA가 가능하지는 않습니다. 그러므로 행렬 곱셈에는 교환법칙이 성립하지 않습니다.
벡터와 행렬의 곱셈
벡터 u = [x,y,z], A = [[A11, A12, A13], [A21, A22, A23], [A31, A32, A33]] 일 때, uA = xA1,* + yA2,* + zA3,* 로 표기할 수 있습니다. 이 식의 경우 선형결합(linear combination) 이라고 부릅니다.
벡터 x 행렬 곱 uA 가 행렬 A의 행벡터들과 벡터 u로 주어진 스칼라 계수 x,y,z의 선형결합에 해당함을 의미합니다. 일반화하면, 1 x n 행벡터 u와 어떤 n x m 행렬 A에 대해 곱 uA는 A의 행벡터들과 u의 스칼라 계수들의 선형결합입니다.
결합법칙
앞서서 행렬 곱셈에는 교환법칙이 성립하지 않는다고 했습니다. 하지만, 몇 가지 편리한 대수(algebra)적 성질들이 존재하며 다음과 같습니다 :
- 덧셈에 대한 분배법칙 : A(B + C) = AB + AC이고 (A + B)C = AC + BC
- 결합법칙 : (AB)C = A(BC)
특히, 결합법칙을 만족하기 때문에 행렬들을 곱하는 순서들을 적절히 선택할 수 있습니다.
전치행렬
행렬의 전치(transpose), 즉 전치행렬은 행렬의 행들과 열들을 맞바꾼 것입니다. m x n 행렬의 전치는 n x m 행렬이 됩니다. 행렬 M에 대해서 전치행렬은 MT로 표기합니다.

전치행렬에는 다음과 같은 성질들이 있습니다 :
- (A + B)T = AT + BT
- (cA)T = CAT
- (AB)T = BTAT
- (AT)T = A
- *(A-1)T = *(AT)-1
단위행렬

단위 행렬(identity matrix) 이라고 부르는 특별한 행렬도 있습니다. 열 수 와 행 수가 같은 정사각형의 행렬을 정방행렬(square matrix) 라고 부르고, 정방행렬에서 좌상에서 우하로의 주대각선에 있는 성분들을 주대각(main diagonal) 성분 이라고 하는데, 단위행렬은 주대각 성분이 모두 1이고, 나머지는 전부 0인 정방행렬을 뜻합니다.
단위행렬은 곱셈의 항등원 역할을 합니다. 즉, A가 m x n 행렬이고 B가 n x p 행렬, I가 n x n 단위행렬이면 반드시
AI = A이고 IB = B
입니다. 즉, 어떤 행렬에 단위행렬을 곱해도 그 행렬은 변하지 않습니다. 쉽게 숫자 1의 행렬버전이라고 생각하시면 됩니다. 특히 행렬 M이 정방행렬이면 단위행렬 곱셈은 교환법칙을 만족합니다.
MI = IM = M
행렬식

행렬식(determinant) 은 정방행렬을 입력받아서 실숫값을 출력하는 특별한 함수입니다. 정방행렬 A의 행렬식을 흔히 det A로 표기합니다.
행렬식은 기하학적으로 행렬식이 3차원 입체의 부피와 관련이 있다는 것과 선형변환 하에서 부피가 변하는 방식에 대한 정보를 제공한다는 점을 증명하는 것이 가능합니다. 또한, 크라메르의 법칙(Cramer's rule; 크라메르 공식) 을 이용해서 1차 연립방정식을 푸는 데에도 쓰입니다.
여기서는 행렬식을 행렬의 역을 구하기 위해 소개합니다. 행렬식에 대한 다음의 정리가 있습니다 :
정방행렬 A는 det A ≠ 0이면 가역행렬(역행렬이 존재하는 행렬)이다.
이 정리를 이용하면 주어진 행렬의 역을 구하는 것이 가능한지를 알 수 있습니다.
소행렬

행렬식을 정의하기 이전에 소행렬의 개념부터 살펴보겠습니다. n x n 행렬 A가 주어졌을 때, 소행렬(minor matrix) Āij는 A의 i번째 행과 j번째 열을 삭제해서 나온 (n-1) x (n-1) 행렬입니다.
행렬식의 정의
행렬의 행렬식은 재귀적으로 정의됩니다. 예를 들어 4 x 4 행렬의 행렬식은 3 x 3 행렬의 행렬식들로 정의되고, 3 x 3 행렬의 행렬식은 2 x 2 행렬의 행렬식들로, 2 x 2 행렬의 행렬식은 1 x 1 행렬의 행렬식들로 정의됩니다( 1 x 1 행렬 A의 행렬식 det A = A11입니다).
A 가 n x n 행렬이고 n > 1이라고 할 때, A의 행렬식은 다음과 같이 정의됩니다.
det A = Σ(j = 1 ~ n) Aij * (-1)(1+j) * det Ā1j
2 x 2 행렬의 행렬식은 다음과 같은 공식이 나옵니다 :

3 x 3 행렬의 행렬식은 다음과 같은 공식을 얻을 수 있습니다 :

4 x 4 행렬의 행렬식은 다음과 같습니다 :

3차원 그래픽에서는 주로 4 x 4 행렬을 다루므로, n > 4에 대한 공식들을 나열하지는 않겠습니다.
딸림행렬

A가 n x n 행렬이라고 할 떄, 곱 Cij = (-1)(i+j) detĀij를 Aij의 여인수(cofactor; 또는 여인자) 라고 합니다. A의 각 성분의 Cij를 계산해서 해당 ij번째 위치에 배치한 행렬 CA를 행렬 A의 여인수행렬(cofactor matrix) 라고 합니다.
또한 이 CA의 전치행렬을 A의 딸림행렬(adjoint matrix; 수반행렬) 이라고 부르고 다음과 같이 표기합니다 :
A* = CAT
딸림행렬을 이용하여 행렬의 역을 계산하는 명시적 공식을 구할 수 있습니다.
역행렬

행렬 대수는 나눗셈 연산을 정의하지 않지만, 곱셈의 역원은 정의합니다. 행렬 대수에서 곱셈의 역원을 행렬의 역(inverse) 또는 역행렬 이라고 부릅니다. 역행렬에 대한 정리는 다음과 같습니다 :
- 역행렬은 정방행렬에만 있습니다. 따라서 역행렬에 대한 논의는 해당 행렬이 정방행렬임을 암묵적으로 가정합니다.
- n x n 행렬 M의 역은 n x n 행렬이며, M^-1로 표기합니다.
- 모든 정방행렬에 역행렬이 있는 것은 아닙니다. 역행렬이 있는 행렬을 가역행렬(invertible matrix) 이라고 부르고, 역행렬이 없는 행렬을 특이행렬(singular matrix) 이라고 부릅니다.
- 역행렬이 존재하는 경우, 그 역행렬은 고유합니다.
- 행렬에 그 역행렬을 곱하면 단위행렬(I)이 나옵니다. 즉, MM-1 = M-1M = I** 입니다. 행렬과 그 역행렬의 곱셈은 행렬 곱셈에서 교환법칙이 성립하는 특별한 사례 중 하나임에 주목하셔야 합니다.
행렬의 역은 행렬 방정식을 만족하는 행렬들을 구할 떄 유용합니다. 예를 들어, p` = pM 이라는 행렬 방정식에서 p` 과 M을 알고 있고 p를 구해야할 때, M이 가역행렬이면 p를 다음과 같이 구할 수 있습니다 :
p` = pM
p`M-1 = pMM-1 등식의 양변에 M-1을 곱합니다.
p`M-1 = pI 역행렬의 정의에 의해 MM-1 = I가 됩니다.
p`M-1 = p 단위행렬의 정의에 의해 pI = p입니다.
딸림행렬과 행렬식을 이용하여 역행렬을 구할 수 있으며 식은 다음과 같습니다 :
A-1 = A* / detA
식이 복잡할 수 있는데 중등 교육 때 배운 2 x 2 행렬의 역행렬 구하는 방법을 떠올리시면 어느 정도 이해가 될 거라 생각합니다.
참고사항
작은 행렬(4 x 4 행렬 이하)의 경우 딸림행렬을 이용한 계산법이 효율적입니다. 더 큰 행렬에서는 가우스 소거법 같은 다른 방법이 쓰입니다. 3차원 그래픽에서 주로 다루는 행렬들은 역행렬 공식을 미리 알 수 있는 특별한 형태이기 때문에, 굳이 일반적인 행렬의 역행렬을 구하는 공식을 사용해서 CPU 주기를 낭비할 필요가 없습니다. 따라서 위의 역행렬 공식을 실제로 적용하는 경우는 거의 없습니다.
행렬 곱의 역행렬에 대한 대수적 성질 하나는 A와 B가 같은 차원의 가역 정방행렬일 때 다음이 성립한다는 것입니다 :
(AB)-1 = B-1A-1
위 식에 대한 증명은 (AB)(B-1A-1) = I 이면서 (B-1A-1)(AB) = I 임을 보임으로써 가능합니다.
(AB)(B-1A-1) = A(BB-1)A-1 = AIA-1 = AA-1 = I
(B-1A-1)(AB) = B-1(A-1A)B = B-1IB = B-1B = I
레퍼런스
정보참조
DirectX 12를 이용한 3D 게임 프로그래밍 입문
위키피디아 - 행렬
수학방
그림참조
그림1 - http://tcpschool.com/codingmath/matrix
그림2 - http://www.ktword.co.kr/word/abbr_view.php?m_temp1=2439
그림3 - https://bishnu.synology.me/wordpress/2015/02/05/%EC%84%A0%ED%98%95-%EB%8C%80%EC%88%98%ED%95%99-%EB%A6%AC%EB%B7%B0-optional-2/
그림4 - https://ko.wikipedia.org/wiki/%ED%96%89%EB%A0%AC%EC%8B%9D
그림5 - http://mathworld.wolfram.com/Minor.html
그림9 - http://blog.naver.com/PostView.nhn?blogId=mykepzzang&logNo=221080868879&parentCategoryNo=44&categoryNo=&viewDate=&isShowPopularPosts=true&from=search
그림10 - https://rfriend.tistory.com/142
- Total
- Today
- Yesterday
- Auto
- P4 Streams
- 행렬
- 언리얼 엔진 5
- 언리얼 엔진
- 구간합
- MSVC C1083
- C# 익명함수
- C++ Compile error
- Perforce Streams
- game hot reload
- Perforce Stream
- visual studio hot reload
- 퍼포스 스트림
- visual studio 핫 리로드
- C# lambda expression
- 알고리즘
- C++
- C# 람다식
- delaying 2 processes from spawning due to memory pressure
- c++ 핫 리로드
- Visual Studio C1083
- 퍼포스 개요
- Unreal Engine 5
- P4 Stream
- GoogleTest
- DXGI
- c++ hot reload
- C7568
- UE4
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
