티스토리 뷰
이번 포스팅에서는 행렬의 곱셈의 구현과 최적화 방법에 대해서만 집중적으로 분석합니다. 행렬에 관한 내용은 행렬 대수 포스팅을 읽어보시거나 다른 레퍼런스를 확인하시면 되겠습니다.
행렬의 곱셈은 왼쪽 행렬의 i번째 행, j번째 열에 있는 요소에 대해 왼쪽 피연산자 행렬의 i번째 행과 오른쪽 피연산자 행렬의 j번째 열을 내적한 값을 산출한다고 행렬 대수에서 언급했습니다. 그림으로 나타내면 다음과 같습니다.
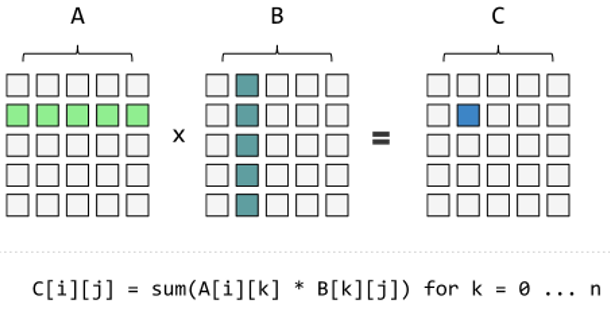
이것을 구현하는 것은 어려운 일이 아닙니다. 빠르게 작성된 행렬 곱셈 연산의 구현은 다음과 같습니다 :
#include <iostream>
using namespace std;
/* 빠르게 작성된 2x2 행렬을 곱하는 코드 */
int main()
{
int a[2][2] = { 1,2,3,4 };
int b[2][2] = { 1,2,3,4 };
int c[2][2] = { 0,0,0,0 };
/* 행렬의 곱 연산을 수행합니다. */
for (int i = 0; i < 2; ++i)
for (int j = 0; j < 2; ++j)
for (int k = 0; k < 2; ++k)
c[i][j] += a[i][k] * b[k][j];
/* 결과값이 담긴 행렬 c를 출력합니다. */
for (int i = 0; i < 2; ++i)
{
for (int j = 0; j < 2; ++j)
cout << c[i][j] << " ";
cout << "\n";
}
}
코드를 보시면 아시겠지만, 행렬 곱셈 연산은 O(n3)임을 알 수 있습니다. 이 알고리즘은 저희가 행렬 곱셈 연산을 수행하는 순서와 다른 것이 없습니다.
코드 자체는 하드코딩되어 있지만, 실행해보면 결과값은 잘 나옵니다. 하지만 단순한 방식의 행렬 곱셈 구현은 행렬의 크기가 커질수록 비효율적인 연산을 수행하게 됩니다.
그 이유는 바로 Cache에 대한 이해가 없이 작성된 코드이기 때문입니다. 컴퓨터 구조를 공부하신 분들은 아시겠지만 비용의 한계로 인해 메모리의 크기는 유한하며, 캐시 역시 이 한계에서 벗어날 수 없습니다(캐시에 대한 내용은 직접 찾아보시길 권합니다).
위 코드의 3번째 for문 내의 b[k][j]를 보면 알 수 있지만, 루프 인덱스 k가 증가할수록 b[k][j]를 참조하기 위해 j * sizeof (int) 만큼 점프해야 합니다. 지금의 경우 8바이트를 뛰겠지만, N이 만약 1000이라면 캐시 메모리에서 4000 바이트를 이동해야 하며, 캐시의 지역성을 만족하지 않게 됩니다.
단순 해법
이 항목에서 적혀있는 최적화된 코드는 엄밀히 완벽하게 최적화된 코드가 아닙니다. 기존의 코드에 비해서 개선이 된 것은 맞지만 가장 빠른 코드는 아니며, 여기서 제시하는 이유는 PS 등의 구현에 사용하는 정도로 적합하다는 의미입니다.
so_sal블로그에서는 행렬 곱셈 연산 시에 인덱스의 배치에 따른 속도차이에 대한 글을 포스팅하고 있습니다. 이것을 참조하여, 부연 설명을 더하고자 합니다.
Matrix multiplication와 index에 따른 속도차이
/* * http://sosal.kr/ * made by so_Sal */ Matrix Multiplication (매트릭스 행렬 곱연산)은 사실 어려운 개념은 아닙니다. 중학교? 쯤에 배웠던것 같은데, 이 개념을 바로 프로그래밍에 써먹기도 그다지 어렵진..
sosal.kr
위 블로그에서는 KIJ 및 IKJ 인덱스 배치 순서가 가장 빠르다고 언급하셨기 때문에 이 중 KIJ 인덱스 배치를 통한 행렬 곱셈 연산 방법을 구현하고자 합니다(매개변수를 보시면 아시겠지만 5x5 행렬에 대한 하드코드 된 곱셈이므로, 일반적으로 사용하기 위해서는 2차 포인터를 이용하여 구현하시면 되겠습니다) :
/* k, i, j 인덱스 배치를 통한 행렬 곱 계산 */
void Multiply(int N, const int(&a)[5][5], const int(&b)[5][5], int(&c)[5][5])
{
for (int k = 0; k < N; ++k)
{
for (int i = 0; i < N; ++i)
{
int Temp = a[i][k];
for (int j = 0; j < N; ++j)
{
c[i][j] += Temp * b[k][j];
}
}
}
}
주의할 점은 += 연산자이기 때문에 결과 행렬 c에 대해서 미리 0으로 초기화를 수행해야 합니다.
이 식을 보았을 때, 바로 계산 순서가 이해가 안 될 수도 있습니다. 저 역시 식만으로는 직관이 힘들었기 때문에 2x2 행렬에 대한 곱셈을 예로 하는 그림을 첨부합니다.

위 코드에 대한 계산 순서는 다음과 같이 이뤄집니다. 우측 행렬인 b행렬 및 c행렬이 캐시의 지역성을 만족하면서 i,j 루프를 돕니다. 이번에는 행렬 a에서 행을 뛰어넘으며 계산하지만, 이전의 IJK 인덱스 배치에서의 행렬 b가 뛰어넘는 것만큼 빈번하게 발생하지는 않는다는 것을 확인할 수 있습니다.
각 인덱스 배치에 대한 연산 속도의 차이는 여기에서 확인하실 수 있습니다.
심화
앞서 말씀드렸듯이, 개선된 코드는 완벽하지 않습니다. 슈트라센 알고리즘을 사용한 것도 아니며, 단순히 지역성을 증가시켰을 뿐입니다. 게다가 100 x 100 이하의 곱셈에서는 캐시의 지역성이 크게 수행속도에 영향을 미치지 않는다고 합니다.
아래의 레퍼런스에서는 이것에 대한 더 깊은 주제로 설명하고 있습니다. 관심 있으신 분들은 살펴보시는 것을 추천드립니다.
stackoverflow - optimized matrix multiplication in c
wikipedia - loop nest optimization
레퍼런스
문서에 대한 레퍼런스
so_sal
위키피디아 - Loop nest optimization
그림에 대한 레퍼런스
그림1 : so_sal
'개발 > Algorithm' 카테고리의 다른 글
| 소수 생성 알고리즘(Prime-generating Algorithm) (1) | 2019.09.14 |
|---|---|
| 순열 알고리즘 (Permutation Algorithm) (3) | 2019.09.06 |
| [C++ STL] 벡터 컨테이너(Vector) (0) | 2019.07.28 |
- Total
- Today
- Yesterday
- Perforce Streams
- C++
- DXGI
- 알고리즘
- C# 람다식
- Perforce Stream
- 언리얼 엔진
- C7568
- 언리얼 엔진 5
- Unreal Engine 5
- 행렬
- visual studio hot reload
- GoogleTest
- visual studio 핫 리로드
- 퍼포스 개요
- P4 Stream
- delaying 2 processes from spawning due to memory pressure
- UE4
- C# lambda expression
- c++ 핫 리로드
- c++ hot reload
- MSVC C1083
- game hot reload
- 구간합
- P4 Streams
- Auto
- C# 익명함수
- Visual Studio C1083
- 퍼포스 스트림
- C++ Compile error
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
