티스토리 뷰
앞서서 펜윅 트리에 대해서 소개한 적이 있습니다[링크]. 위 링크에서 세그먼트 트리와의 비교점 역시 쓰여있으므로, 차이점을 알고 싶으신 분들은 위 링크를 방문해 주시면 되겠습니다. 따라서 이 포스팅에서는 순수하게 세그먼트 트리에 대해서 설명하도록 하겠습니다.
세그먼트 트리 역시 부분합을 빠르게 찾을 수 있는 자료구조입니다. 위키피디아에서는 다음과 같이 정의하고 있습니다 :
통계 트리(statistic tree)라도고 하는 세그먼트 트리(Segment tree) 는 세그먼트나 간격에 대한 정보를 저장하는 트리 자료구조입니다. 주어진 지점에서 포함된 세그먼트들을 쿼리할 수 있습니다.
이론적으로 정적 구조체이며, 이 말은 한번 만들어지면 수정될 수 없음을 의미합니다. 유사한 데이터 구조로 간격 트리(interval tree) 가 있습니다.
n개의 간격을 가진 I 세트에 대해 O(nlog n) 시간 복잡도로 만들 수 있습니다. 또한 쿼리 지점에 대해 O(log n + k) 시간 복잡도로 탐색할 수 있습니다(이 때 k는 검색된 간격 또는 세그먼트의 수를 의미합니다).
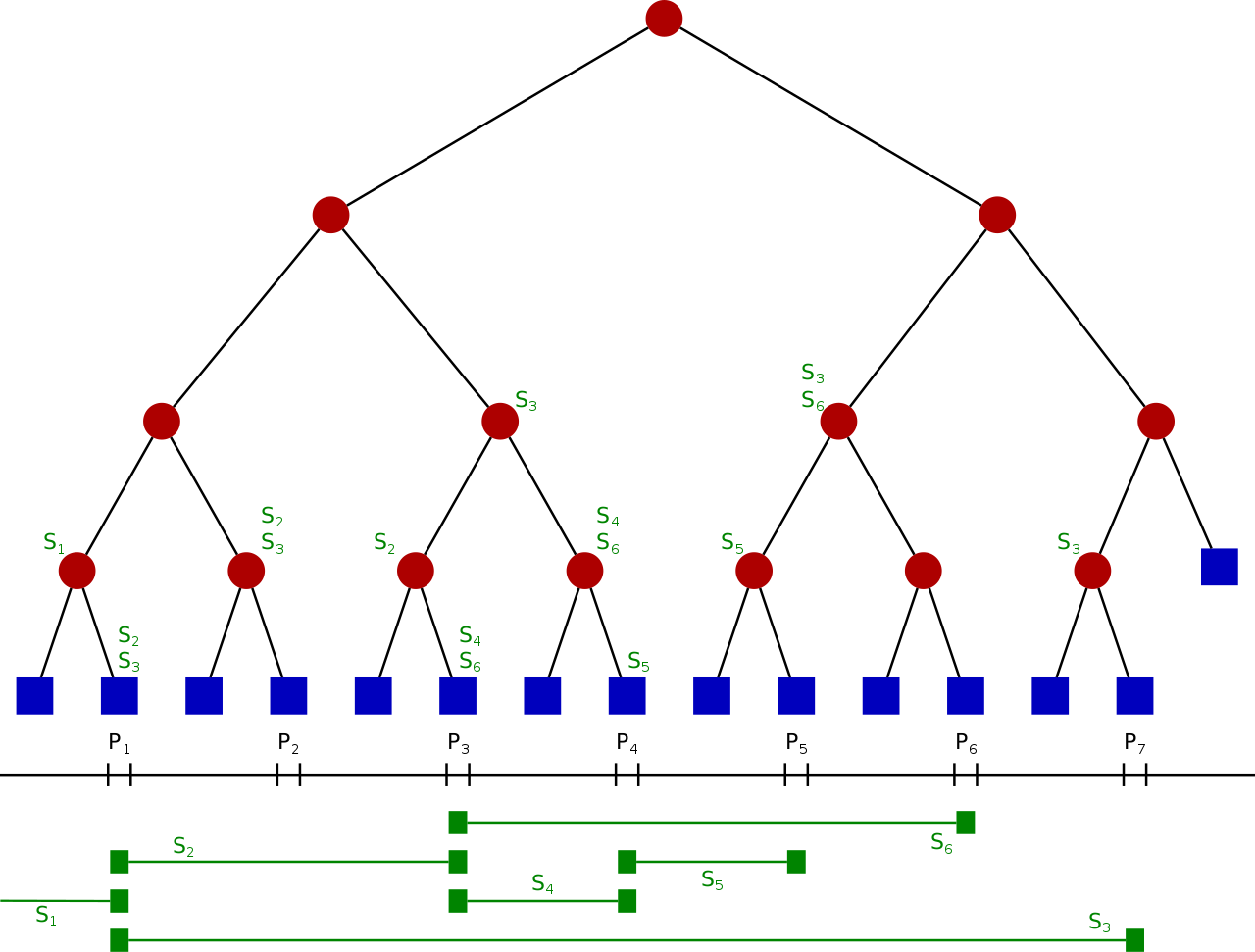
말이 어렵게 되어 있으므로 쉽게 설명하자면, 펜윅 트리와 비슷합니다. 사용 용도는 다음과 같습니다 :
- 요소들의 구간합을 구하는 경우
- 특정 구간에서 가장 큰 값 또는 작은 값을 구하는 경우
- 특정 구간에 대한 정보를 필요로 하는 경우
이번 포스팅에서는 그 중, 기초적인 구간합에 대한 쿼리를 다루도록 하겠습니다.
세그먼트 트리의 구조


그림 2에서 보듯이 세그먼트의 트리는 대부분 완전 이진 트리(아닐 수도 있다는 의미입니다(크기 n이 6일 때))로 비단말 노드가 자식 노드들의 합을 가지는 형태로 구성됩니다. 이렇게 함으로써 특정 구간에 대한 검색을 n 크기의 입력에 대해 O(log n) 시간복잡도로 검색할 수 있습니다.
세그먼트 트리의 요구 크기
세그먼트 트리가 힙의 구현처럼 배열을 사용하여 구현하기 때문에 세그먼트 트리의 전체 크기를 알아서 지정해야할 필요가 있습니다.
이 경우, 세그먼트 트리의 요구 크기를 구하는 방법은 crocus님께서 쓰신 글을 인용합니다 :
아래 init함수를 만들기 전에 우선 하나 알고 가야할 사실이 있다.
N = 12일 때의 세그먼트 트리의 전체 크기(배열 사이즈 정하기)를 구하기 위해서는
2k로 12보다 바로 큰 값을 만들 수 있는 k를 찾아야한다. 즉, k는 4이다.
그리고 난 뒤 2k를 하면 16이 되고 16에 * 2를 하면 우리가 원하는 세그먼트 트리의 크기를 구할 수 있다.이 과정이 귀찮다면 그냥 N * 4를하면(여기서는 48이 세그먼트 트리 크기가 될 것이다.)
메모리는 조금 더 먹지만, 편리하게 이용할 수 있다.

세그먼트 트리를 메모리 구조의 관점에서 살펴 보면 다음과 같이 구성됩니다(그림의 설명대로 따라가기 위해 1번째 인덱스를 1로 합니다).
다른 완전 이진 트리와 마찬가지로 모든 자식 노드 c의 부모 노드 p는 p = c / 2로 찾을 수 있습니다. 반대로 의미하자면, 부모 노드 p의 자식 노드 c1, c2는 각각 c1 = p * 2, c2 = p * 2 + 1로 찾을 수 있습니다(만약 시작 인덱스가 0이면 그에 맞게 위 식들을 수정해 줘야 합니다).
알아두셔야할 점은 앞의 인용문에서 N = 12일 때, 세그먼트 크기가 32라고 했을 때에도, 온전히 메모리 전부를 사용하는 것은 아닙니다. 가령 입력 크기 n = 6인 배열에 대해 세그먼트 메모리 표현은 다음과 같습니다 :
아래는 입력 배열 {1, 3, 5, 7, 9, 11}에 대한 세그먼트 트리의 메모리 표현입니다.
세그먼트 메모리 = {36, 9, 27, 4, 5, 16, 11, 1, 3, DUMMY, DUMMY, 7, 9, DUMMY, DUMMY}
여기서 DUMMY 값은 액세스되지 않으며 사용되지 않습니다. 이러한 부분은 공간 낭비로 이어지며, 코드를 최적화 하여 메모리 낭비를 줄일 수 있지만, 아래에서 설명할 구간합 구하기 및 구간합 갱신 의 코드 구현이 더 복잡해집니다.
세그먼트 트리의 합
세그먼트 트리의 구간합은 인덱스에 저장된 값들을 이용하여 구할 수 있습니다. 그림 3의 세그먼트 트리에 대하여 예시를 들겠습니다.
case 1 : 0 ~ 3번 인덱스까지의 합 구하기
위 값은 2번 노드에서 이미 값을 구해놓았습니다. 따라서, 합이 16임을 알 수 있습니다.
case 2 : 0 ~ 2번 인덱스까지의 합 구하기
위 값은 0 ~ 3번까지의 합을 의미하는 2번 노드에서 3번의 합을 의미하는 11번 노드를 뺌으로써 구할 수 있습니다. 따라서 16 - 4 = 12임을 알 수 있습니다.
세그먼트 트리의 갱신
세그먼트 트리의 인덱스 중 하나가 값이 바뀌는 경우, 그에 해당하는 리프 노드에서 그 차이(diff)를 루트(또는 루트 노드에서 리프 노드까지)까지 차례대로 더하면서 갱신하면 됩니다. 이에 대해서는 아래 그림으로 설명을 대체하겠습니다.

구현
먼저 기존의 자료들을 트리로 구성해야할 필요가 있습니다. 앞에서 언급했듯이 트리로 만드는 작업이 필요하며, 이번 포스팅에서는 재귀를 이용하여 구현하도록 하겠습니다.
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
// 입력된 배열로부터 세그먼트 트리를 구성합니다(이번 세그먼트 트리에서는 인덱스가 1에서 시작하도록 하였습니다).
int init_stree(vector<int>& stree, vector<int>& data, int node, int begin, int end)
{
if (begin == end)
return stree[node] = data[begin];
int mid = (begin + end) / 2;
return stree[node] = init_stree(stree, data, node * 2, begin, mid) + init_stree(stree, data, node * 2 + 1, mid + 1, end);
}
// 구간합을 구하는 함수입니다.
// 이 때, begin-end 및 left-right는 초기화시 사용된 배열이 [0 , n - 1] 범위를 가졌으므로, 이에 맞춰줘야 합니다.
int sum_stree(vector<int>& stree, int node, int begin, int end, const int left, const int right)
{
if (right < begin || end < left)
return 0;
else if (left <= begin && end <= right)
return stree[node];
else
{
int mid = (begin + end) / 2;
return sum_stree(stree, node * 2, begin, mid, left, right) + sum_stree(stree, node * 2 + 1, mid + 1, end, left, right);
}
}
// 세그먼트 트리의 갱신된 값을 반영하는 함수입니다.
// index, begin-end는 초기화시 사용된 배열이 [0 , n - 1] 범위를 가졌으므로, 이에 맞춰줘야 합니다.
void update_stree(vector<int>& stree, int node, const int index, const int diff, int begin, int end)
{
if ((begin <= index && index <= end) == false)
return;
stree[node] += diff;
if (begin != end)
{
int mid = (begin + end) / 2;
update_stree(stree, node * 2, index, diff, begin, mid);
update_stree(stree, node * 2 + 1, index, diff, mid + 1, end);
}
}
int main()
{
vector<int> v = { 1,2,3,4,5,6,7,8 };
int stree_size = (int)ceil(log2(v.size()));
vector<int> st(1 << (stree_size + 1));
init_stree(st, v, 1, 0, v.size() - 1);
cout << sum_stree(st, 1, 0, v.size() - 1, 0, 7) << "\n"; // 36
update_stree(st, 1, 0, 2, 0, v.size() - 1);
cout << sum_stree(st, 1, 0, v.size() - 1, 0, 7) << "\n"; // 38
return 0;
}
참고자료
문서 참조
위키피디아 - 세그먼트 트리
Isu Korea - 세그먼트 트리 / 인덱스 트리
arkainoh - [Algorithm] 세그먼트 트리 (Segment Tree)
Crocus - 세그먼트 트리(SegmentTree)
GeeksforGeeks - Segment Tree | Set 1 (Sum of given range)
그림 참조
그림1 - https://en.wikipedia.org/wiki/Segment_tree#/media/File:Segment_tree.svg
그림2 -http://isukorea.com/blog/home/waylight3/216
그림3 - http://isukorea.com/blog/home/waylight3/216
그림4 - https://www.crocus.co.kr/648
그림5 -http://isukorea.com/blog/home/waylight3/216
'개발 > Data Structure' 카테고리의 다른 글
| 펜윅 트리(Fenwick Tree, Binary Indexed Tree) (2) | 2019.11.05 |
|---|
- Total
- Today
- Yesterday
- C# 익명함수
- 알고리즘
- 행렬
- Unreal Engine 5
- C++ Compile error
- P4 Streams
- Visual Studio C1083
- c++ 핫 리로드
- 구간합
- UE4
- delaying 2 processes from spawning due to memory pressure
- C7568
- C++
- 언리얼 엔진 5
- Auto
- MSVC C1083
- 언리얼 엔진
- C# 람다식
- Perforce Streams
- game hot reload
- 퍼포스 개요
- P4 Stream
- Perforce Stream
- GoogleTest
- visual studio hot reload
- DXGI
- C# lambda expression
- visual studio 핫 리로드
- 퍼포스 스트림
- c++ hot reload
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
